
 |
Eager Space | Videos by Alpha | Videos by Date | All Video Text | Support | Community | About |
|---|


Starship is a tall and thin vehicle, and it appears to be much tippier than the Apollo lunar module.
Will it fall over when it lands on the moon? Can we figure out how stable it really is?

To answer our question, we will need to build a model of the center of gravity of the starship lander.
When building a model, it's often useful and/or required to make simplifying assumptions to make the calculations possible or - in my case - simple enough that I don't lose interest.
But it's also possible to go too far and end up with a model that is divorced from reality, such as a spherical cow of uniform density.
I'll be pointing out some of my assumptions along the way. Some will be wrong because we don't have enough details about starship, some wrong because I needed to simplify things, and some wrong because I don't understand things well enough.
The goal of this exercise is to create a model that is useful enough to get a sense of the right answer, without using a spherical starship.
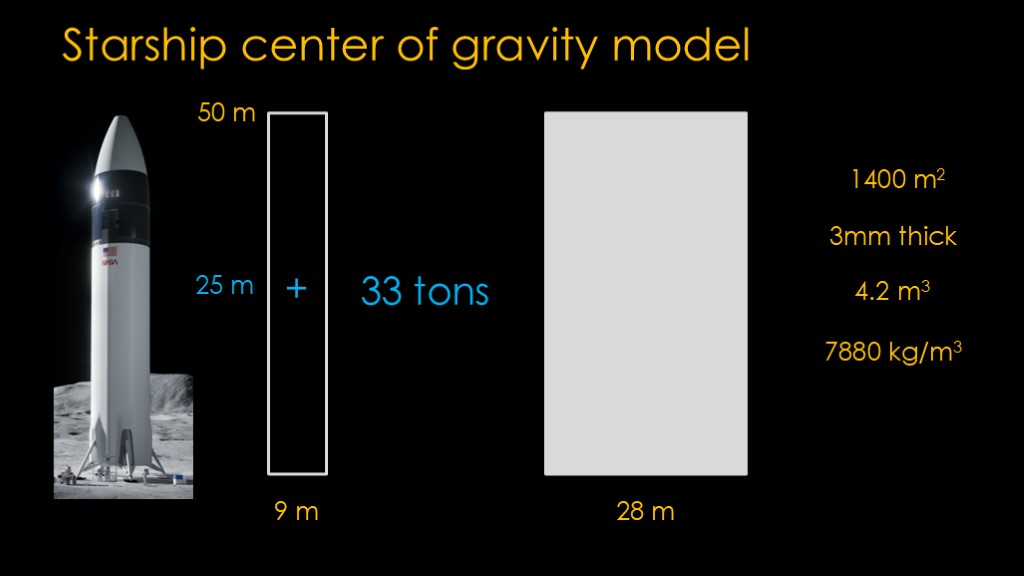
Here's my simplified model...
Starship is a 50 meter tall tube that is 9 meters in diameter.
If we unrolled the stainless steel used to make that tube, it would be 50 meters by 28 meters, for an area of 1400 square meters.
It is made out of stainless steel that is 3 mm thick, and that means it uses 4.2 cubic meters of material.
301 stainless steel has a mass of 7880 kilograms per cubic meter, and therefore the total mass is 33,000 kilograms or 33 tons. The center of gravity is right in the middle of the tube.
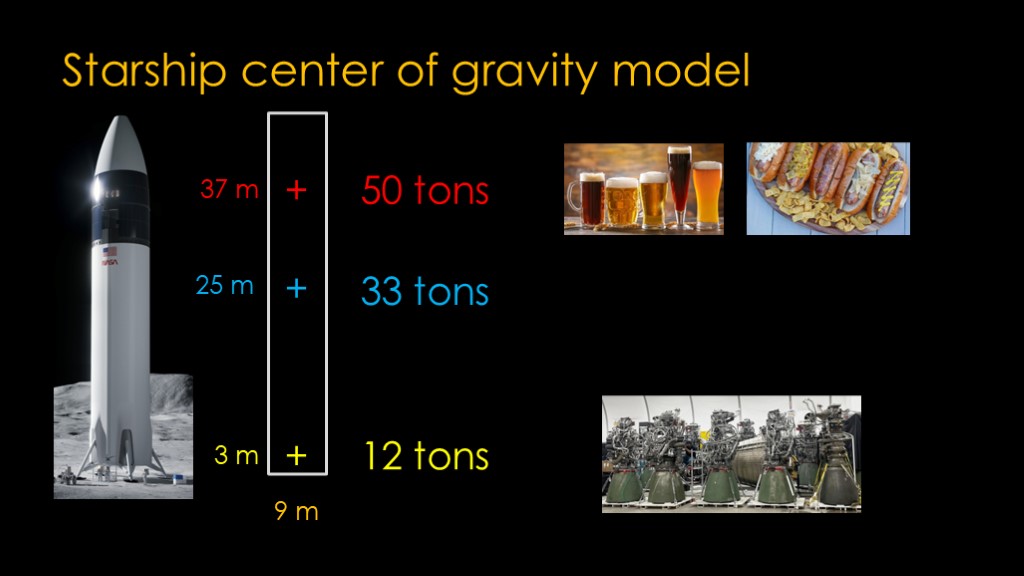
There are two other significant mass concentrations.
There is a payload section that starts roughly 32 meters off the ground, and I'm going to assume the center of mass for the payload is a few meters higher, at 37 meters. The payload is 50 tons, which will leave plenty of room for the most important payload items.
There is engine mass right near the tail, with a center of gravity at around 3 meters. Six engines at about 2 tons each would be 12 tons. And yes, the raptors might be lighter than that, but there's other mass back there as well.
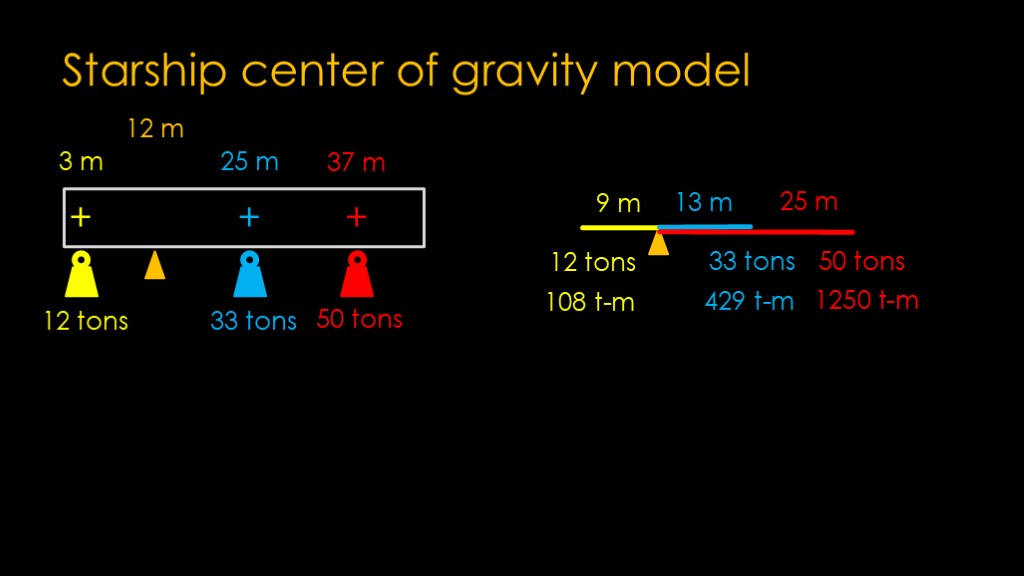
How do we figure out the center of gravity? There are multiple methods, and I've chosen one that I hope is understandable.
We lay the rocket down on its side and treat it like a balance - each of the masses that we calculated are like weights hanging from the rocket at a specific point.
There are 12 tons of engine hanging 3 meters from the left end, 33 tons of structure hanging at the middle at 25 meters, and 50 tons of payload hanging at 37 meters.
Let's say that we add a support point - a fulcrum - 12 meters from the left. Will this balance? Instinctively, we would say that the right side is much heavier. But can we come up with a mathematical solution?
We can express this in terms of torques.
To the left side, we have a weight of 12 tons 9 meters to the left of the fulcrum, giving us a torque of 9 * 12 = 108 ton meters.
On the right side, we have 33 tones 13 meters to the right of the fulcrum, giving us 429 ton meters, and 50 tons 25 meters from the fulcrum, giving us 1250 ton meters.
Clearly this does not balance.
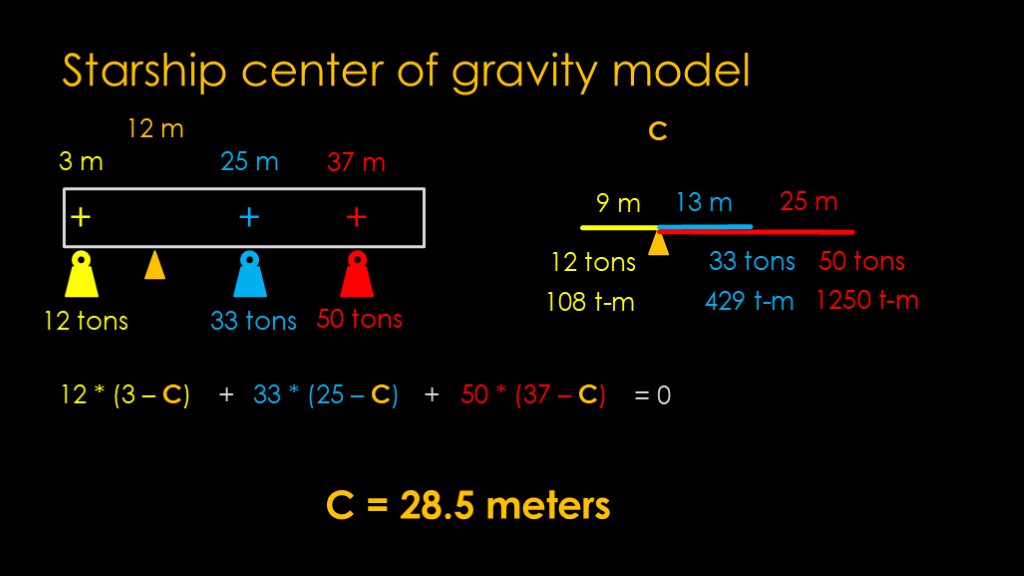
If we define C to be the distance of the fulcrum from the left side, we can write the contribution of each mass in terms of that distance.
For the first term, it is 12 tons * 3 minus C meters. Note that this gives a negative torque because the weight is to the left of the fulcrum.
The vehicle is 33 tons * 25 minus C meters, and the payload 50 tons times 37 minus C meters.
Add these up, and we get the net torque - how much the forces are twisting the rocket. Our goal is for all those forces to balance and for the net torque to be zero.
I'll skip simplifying the equation to solve for C - I did it by hand but wolfram alpha would be happy to help you out - and the answer is 28.5 meters.
The center of gravity of starship is 28.5 meters up from the bottom of the rocket.
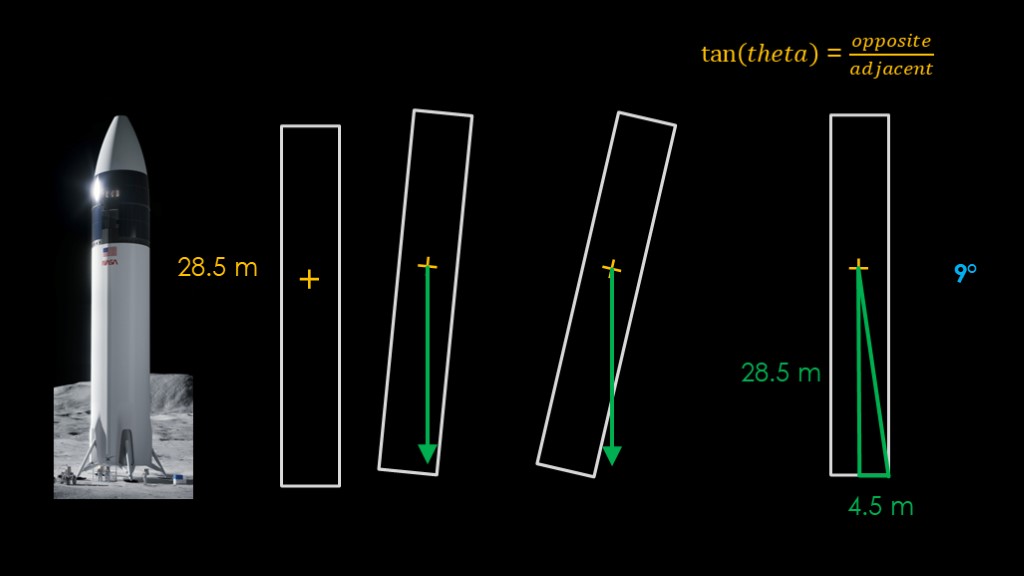
Now that we've figured out the rough center of gravity, we can figure out how stable starship will be.
This is actually pretty simple - as long as a vertical line from the center of gravity to the bottom of the rocket is inside the base of the rocket, it will be stable.
As soon as it moves outside the base, bad things will happen.
We can find the threshold - what I'll call the critical angle - by drawing the following triangle. The vertical distance is 28.5 meters, the horizontal distance is half the diameter, for 4.5m.
I'm sure everybody remembers from their high school trigonometry that the tangent of the angle is equal to the length of the opposite side divided by the length of the adjacent side, and from that we can calculate that the angle is 9 degrees.
Which would seem to validate our belief that starship makes a tippy lander.
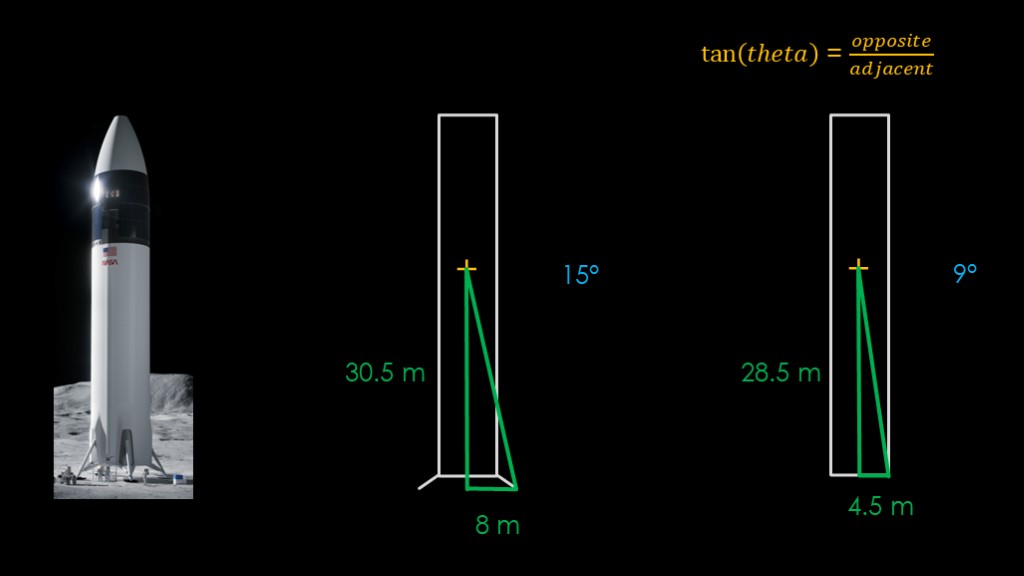
I'm guessing that some of you noticed that I forget the landing legs, which was deliberate.
All we know about the legs is renders like this one and that's hardly definitive, but based on what we see here, I estimate that the base diameter of the legs is 16 meters and that the legs raise the body of the rocket by 2 meters.
That changes the side of the triangle to 30.5 meters and the base to 8 meters. We can redo the calculation, and we get an answer of 15 degrees.
And therefore we can definitely say that Starship can lean at up to 15 degrees before it falls over, and we have finished our discus...
Yes, you in the back, with your hand up. What do you want?
What do you mean "what about the propellant?" Yes, yes, starship needs to have propellant to get back into orbit, but how could we possibly figure that...
The rocket equation? Okay, we'll try that.

We need to figure out how much propellant starship will have in its tanks when it lands on the moon. If you want to understand more about the upcoming calculations, see "planning your solar system road trip".
The required delta v to get from the lunar surface to a 100 km orbit is about 1800 meters per second, and getting to near rectilinear halo orbit is another 450 meters per second, for a total of 2250 meters per second.
Here's that rocket equation.
We refactor to solve for the mass ratio.
Plug in the delta v that we need and the specific impulse of the raptor engine, 363.
And we find that the mass ratio needs to be 1.88
In our model, the dry mass is 95 tons, so to get that mass ratio we need 84 tons of propellant.
We know the mixture ratio of the raptor is 3.6 parts liquid oxygen to 1 part liquid methane, and that comes out to 78% liquid oxygen and 22% liquid methane, or 65.5 tons of liquid oxygen and 18.5 tons of liquid methane.
That is the minimal amount of propellant that the lunar starship will need to get back into orbit.
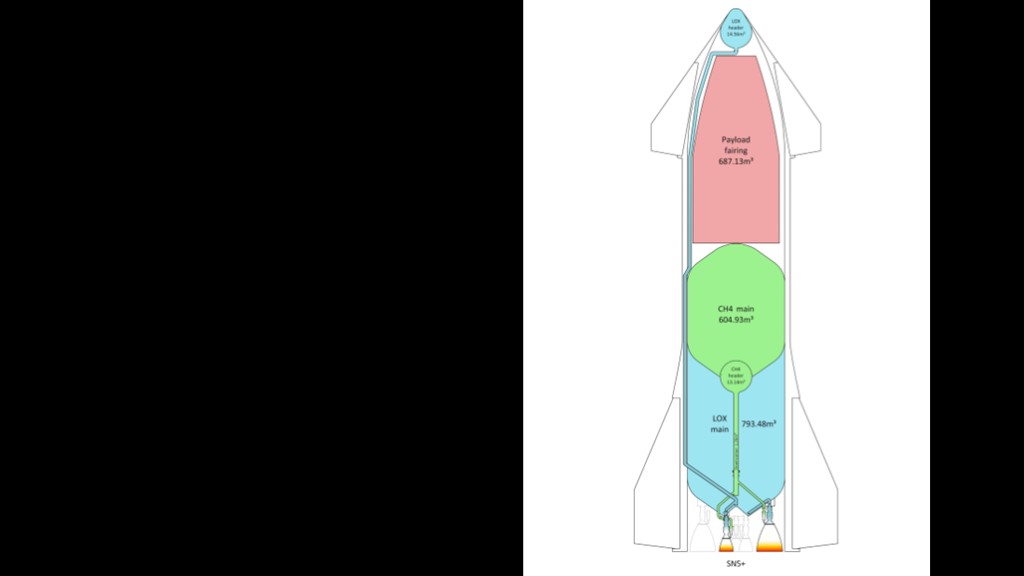

How much does that fill the tanks?
65.5 tons of liquid oxygen at a density of 1142 kilograms per cubic meter means that we have 57 cubic meters of liquid oxygen, and in a 9 meter tank that is 0.9 meters tall.
18.5 tons of liquid methane at a density of 439 kilograms per cubic meter means we have 42 cubic meters of liquid methane, and in a 9 meter tank that is 0.66 meters tall.
Basing the tank locations on drawings of starship, that adds 66 tons of mass at 5.5 meters and 19 tons of mass at 17.3 meters.
Do the calculation, and we find that the center of mass is now 19 meters off the ground, or nearly 10 meters lower.
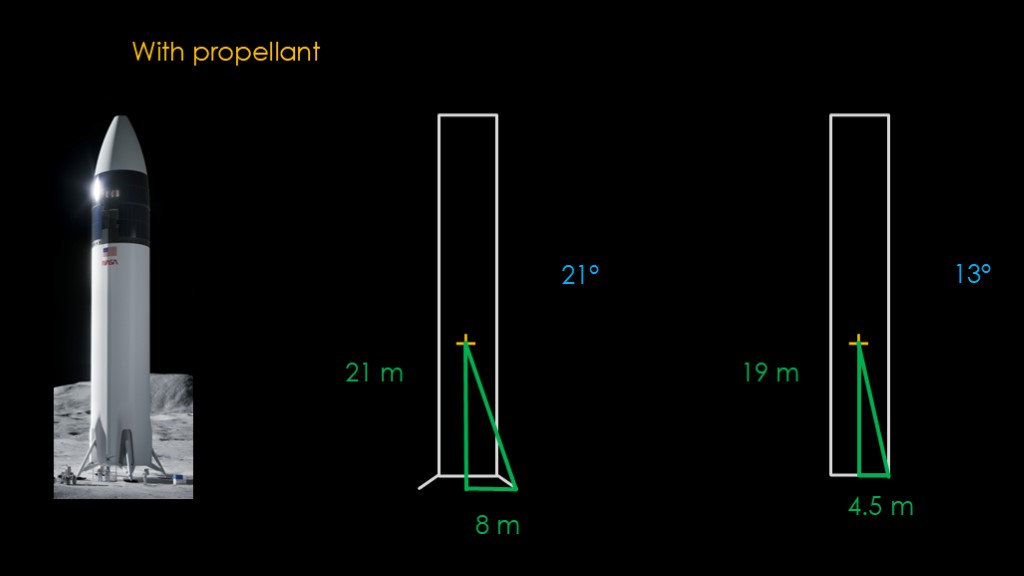
Redoing our calculations with the lower center of gravity, we find that a starship without legs can tilt up to 13 degrees without falling over, and one with legs can tilt 21 degrees.
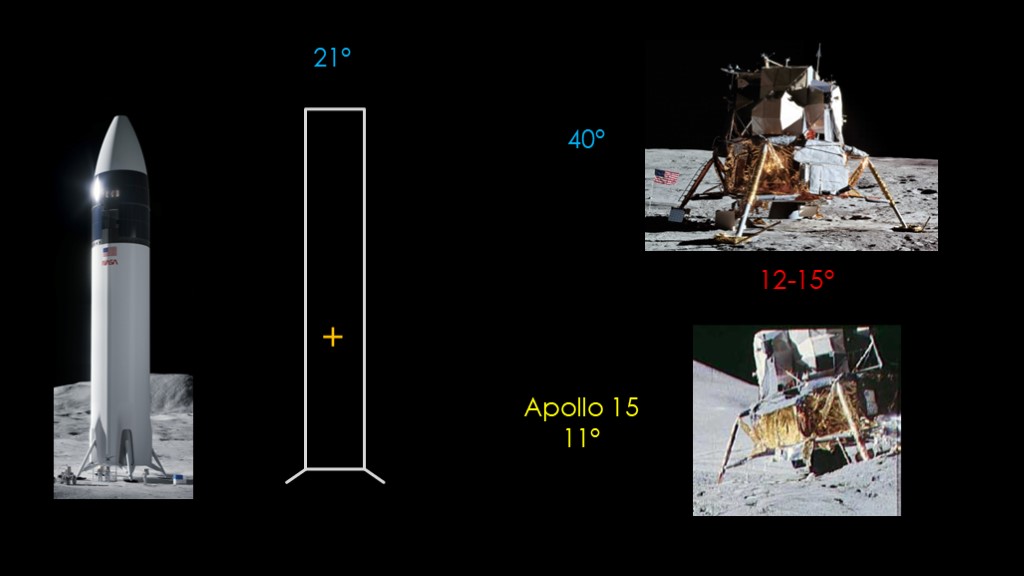
How does this angle compare to Apollo?
The Apollo LEM was quite resistant to tip-over, requiring a full 40 degrees before it would tip over. Which is quite a bit higher than lunar starship.
But the LEM had a takeoff limit of either 12 or 15 degrees depending on who you listen to. Which seems pretty high, but on Apollo 15 the LEM ended up at an angle of 11 degrees, which is close to the limit.

Will lunar starship tip over?
Starship has a low center of gravity and would need to land at an angle of more than 20 degrees to be in danger, and that seems unlikely.

If you enjoyed this video, conduct your own stability experiments using an empty paper towel tube, four quail eggs, and 135 cc of chicken broth.